Overview
Non-Linear Dimensionality Reduction (NLDR) techniques such as ISOMAP, LLE, Laplacian Eigenmaps etc. attempt to estimate low-dimensional latent descriptors for data assumed to be drawn from an m-dimensional manifold in an ambient n-dimensional space. Out-of-Sample Extension - the problem of estimating the latent vectors for novel data - has attracted considerable attention in the literature. Here we consider the opposite problem, that of reconstructing new high-dimensional points, given a novel latent-vector in a previously discovered embedding. Such a procedure finds relevance in applications such as video frame interpolation or robot motion planning.
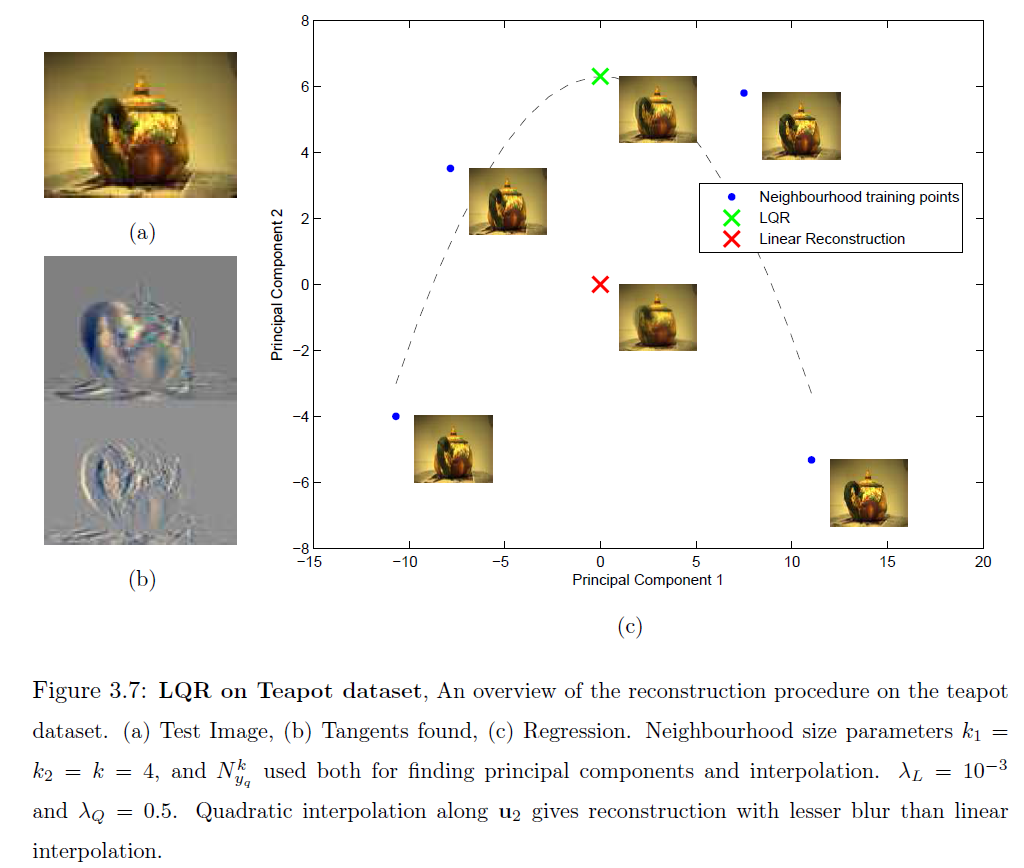
Some global methods can be applied to the problem, but these are polynomials on the total number of data points N resulting in a complexity of O(N3), where N is often in the thousands. In contrast, we propose a Local Quadrature Reconstruction (LQR) approach that looks at only the local k-neighbourhood for which the complexity reduces to O(k3) (k may be about 10). LQR achieves low error by estimating the second order error terms based on a differential geometric formulation for a small neighbourhood around the query point on the manifold. Main features of LQR include its fast reconstruction time and lack of a training phase, but since k increases as O(m2) it is currently limited to manifolds with low intrinsic dimension.