Interval Algebra: A review

This page summarizes different aspects of interval algebra:

What is Interval Algebra?

Interval = Ordered pair of points

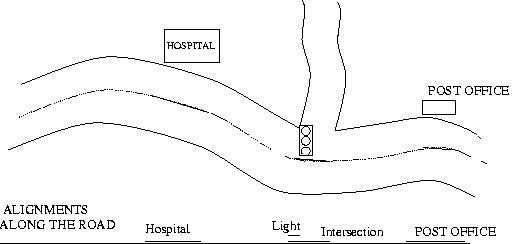
1-D interval - along any nominal axis, e.g. the center-line of a road:

Intervals along the road centerline (in meters):
"Light" = [311.2,311.3]
"Intersection" = [311.2,317.4]

Abstraction:
      
  • "There is a light at the start of the intersection."
  • "The light [interval] starts the intersection [interval]."

    • Formalism:

    Sign Algebra: x IN (-, 0, +)

    1-D Point Algebra: Given two ordered points x,y, relation between x and y is IN (-, 0, +). nif x is before y then the relation is written as x < y or x (-) y

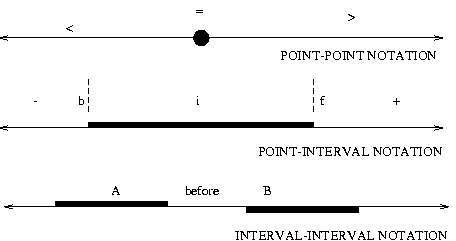
    DEFINITION:

    Interval:[a,b], where a < b

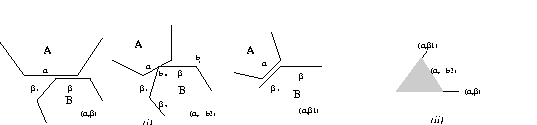
    Note that intervals may arise in any domain with ordered motion. For example, in analyzing the motion of bodies in contact, the concept of Contact Formations captures the intervals of motion for which the qualitative relations remain unaltered. Thus the contact formation [edge(a), vertex(b1)] holds between the point contact states [edge(a),edge(beta)] and [edge(a), edge(beta1)].

    Interval notions can only be applied to rotations over limited ranges.

    Point-Interval Algebra

    Given a point x and an Interval A = [a1,a2], the point x can have 3x3 relations with points a1 and a2. However only five of these are valid since a1 < a2:
    1. x < a1,a2
    2. x = a1, (x < a2)
    3. a1 < x < a2
    4. x = a2, (a1 < x)
    5. x > a2,a1

    Relations between intervals

    Given two intervals A = [a1,a2] and B = [b1,b2], though there are 3^4 = 81 relations between the four points, only 13 of these valid for ordered non-zero intervals.

    As an interval A slies from right to left w.r.t. another interval B, the relation of A w.r.t. B is initially BEFORE (- -). After A OVERLAPS B, the relation can progress along one of three paths depending on the relative sizes of A and B.

    The relations can be expressed as the point-interval relations of the two end-points of A w.r.t. interval B.

    1. BEFORE (- -)
    2. MEETS (- b)
    3. OVERLAPS (-i)
    4. STARTS (bi)
    5. CONTAINED-BY (ii)
    6. FINISHES (if)
    7. EQUALS (bf)
    8. STARTED-BY (i+)
    9. CONTAINS (-+)
    10. FINISHED-BY (-f)
    11. OVERLAPPED-BY (i+)
    12. MET-BY (f+)
    13. AFTER (++)

    Completeness

    THEOREM: All relations that can be expressed between the endpoints of intervals in sign algebra can also be expressed in interval algebra.

    This means that all relative positions are preserved, without regard to metrics such as size, distance, etc.

    This is the meaning in which Interval algebra is both abstract and complete.

    Why is completeness needed?

    Machine learning is concerned with completeness, so that no critical aspect of a problem is overlooked.

    For example, in these images of blocks, relations such as the blocks must touch in Z cannot be missed out by the representation. Similarly, in the famous ARCH learning paradigm, the fact that two columns cannot TOUCH must be modeled.

    Yet relations must not be too detailed, which would result in unmanageable search spaces. Interval algebra provides a good compromise between these, since it is non-quantitative and abstract - yet it is complete in the sign algebra of (-,0,+).

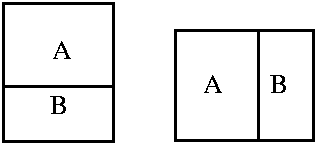
    Another problem with ad hoc abstractions is that underlying relations - such as what is ON from one view may be LEFT-OF in another - is missed out.

    For these reasons Interval Algebra is being increasingly used in reasoning about time, rectangular domains, angular domains etc.

    It is also possible to extend interval algebra to provide some degree of description for relative size, symmetry and relative orientation. Also, in real life, it is necessary to model intervals that are not fixed, but may vary, e.g. "This talk will go on for nearly an hour".

    You may wish to check out this list of links on resources for spatial reasoning.

    C V Publications Research Projects Teaching Students My Other Page Home
    ME Home Page   IITKHome   CFD Lab   ME Faculty

    Latest update: September 18, 1999