 |
 |
| h-symbol: human symbols attach a meaning to each label | f-symbol: formal computer symbols are just the labels |
 |
 |
| h-symbol: human symbols attach a meaning to each label | f-symbol: formal computer symbols are just the labels |
If you ask a designer what a "symbol" is, the answer will usually be that it is a sign that stands for something else. In design discourse, a symbol like gas flow triggers a rich set of associations, which constitutes its semantics. On the other hand, the symbol gas-flow used in computer programs (based in theory on formal logic) is a placeholder for syntactic operations and doesn't "stand for" anything else - any meaning they have is encoded in the relations it has with other symbols. We may consider this analogous to a blind man's knowledge of the colour "red", which may be quite rich - e.g. he may know that red is different from green or that crimson is a kind of red, but his knowledge is limited to such relations, and is not "grounded" in direct perceptual and other experience.
A second difficulty with formal symbols are that they are ultimately defined within the universe of symbols, which means that their definitions are in the end, circular. At the same time, formalisms that deal with perception and other "modes" of cognition, often do not result in symbols. Although there is some who claim a place for "perceptual symbols" (e.g. Barsalou 99), purely perceptual symbols are hard to fix, they may continue to drift based on changing patterns of experience. However, it is now becoming possible to use machine learning approaches to model the process of symbol formation as it happens in humans. Eventually, by deploying such symbols in a social process (e.g. design communication), one may anchor the meaning given to a "public" symbol, at least within a social group. The semantics of the symbol in each user may be somewhat different based on their own experience, but they would still have a large degree of overlap with each other. A major advantage of such grounded symbol systems is that it can make inferences that are not explicitly programmed - e.g. that gas-flow may be similar in some aspects to liquid-flow. More critically, the so-called brittle failures experienced in formal symbol ontologies is unlikely to occur if symbols are associated with rich sensorimotor linkages.In the "infant designer enterprise", our objective is to discover symbolic knowledge about the design domain via explorations in the design space. Initially, the infant designer is exposed only to problems that are well-understood. Thus problems it considers are those for which the set of design variables, as well as the measures of performance are given. Based on this input, it explores the space of "good designs", or the Functionally Feasible Regions (FFRs). In many situations, these spaces occupy only a small fraction of the design space (otherwise the design problem would be too simple). The infant designer seeks to find compact encodings for the FFRs, so that it can represent the design using fewer bits of information. Computational analogs of this process involve trying to reduce the dimensionality of the space in which the FFRs lie. The result is that the system builds up considerable amounts of domain knowledge, though at this stage this knowledge may be implicit (sub-symbolic).
We demonstrate this process with the infant designer address some extremely simple problems, such as learning the the notion of containment - rules like "a cavity can hold only objects that are smaller", and show how this can lead to the concepts such as clearance and tight fit. These grounded models constitute an abstraction in the design space, which may be thought of as an image schema or the semantic pole of an incipient symbol. We believe that in order to eventually build systems that can generalize and learn about more complex design situations, we must first build such an elementary symbol system, and then expose it to problems of increasingly complexity in order to build a symbol systems that are ultimately grounded in the design experience.
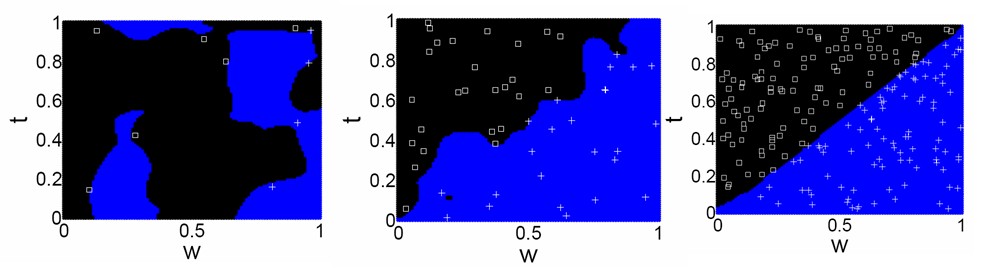 Learning containment. When can a latch of width t (y-axis)
fit a slot of width w(x-axis)? The patterns of successful insertions
(+) versus failures (◊), specifies the Functionally
Feasible Region or FFR (blue area). With little experience (10,50 instances
in a,b), the pattern learned is poor, but the w>t is quite well
learned by (c) 200 instances.
Learning containment. When can a latch of width t (y-axis)
fit a slot of width w(x-axis)? The patterns of successful insertions
(+) versus failures (◊), specifies the Functionally
Feasible Region or FFR (blue area). With little experience (10,50 instances
in a,b), the pattern learned is poor, but the w>t is quite well
learned by (c) 200 instances.
look after the sense, and the sounds will take care of themselves
- Lewis Carroll, Alice in Wonderland
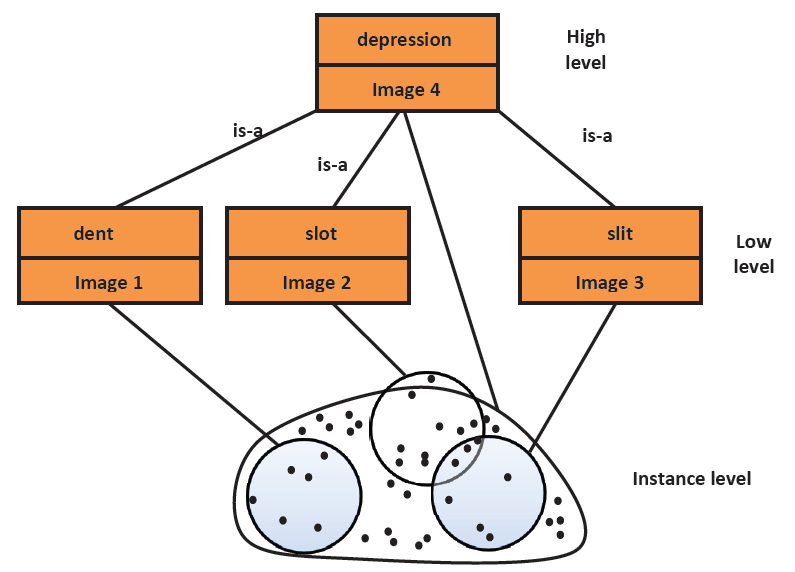
Semantics is relational. The meaning of "dent" depends on other symbols available to us. In a language system without close terms, the interpretation would be broader.
As an example of this process, let us consider a slightly more complex design task, that of the universal motor, which can run on AC or DC. We can formulate the design problem in terms of a number of design variables (eight, say), and a number of design objectives - maximizing torque and efficiency while minimizing weight, say. Now, we can find the set of solutions which cannot be bettered on all counts. These non-dominated solutions lie along a 2-D surface in the 3D objective space (figure below, left). This is the space of "good designs" or the FFRs.
The question we would like to ask is if these "good designs" exhibit some pattern in the original eight-dimensional design space, that would permit dimensionality reduction and the emergence of chunks? In this particular example, even in the 8-D design space, a 2-D manifold appears to fits this data quite well. The pattern of solutions on this manifold can be captured in these two dimensions, which may be thought of as chunks. Each chunk or discovered "feature" represents a complex inter-relation in the original design space that determine where the meaningful designs lie.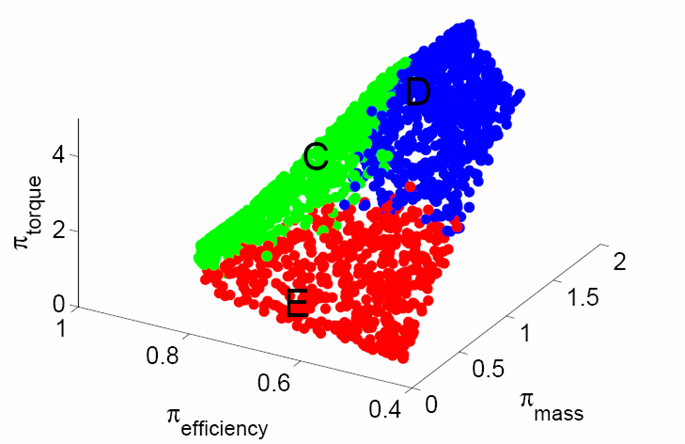
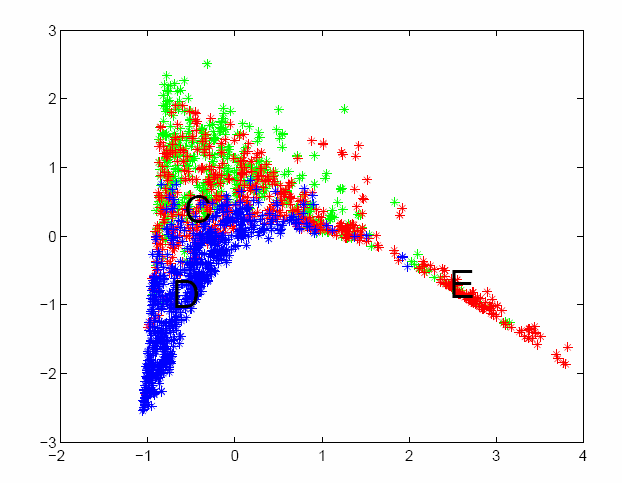
Semantics and Dimensionality Reduction. Universal motor design: 8 design variables, three design objectives. (a) In the 3-D objective space, the "good designs", lie along a 2-D pareto surface. (b) It turns out that even in the 8-D design space, a 2D manifold fits the "good designs" (FFR) quite well.
[More on chunks in the Universal Motor design space.]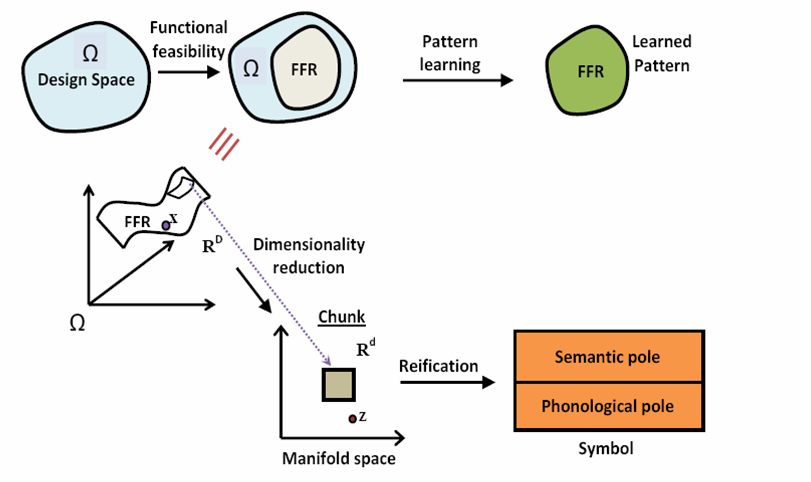
Symbol emergence. The space of "good designs" or the Functionally Feasible Regions (FFR)s constitute narrow regions of the design space, often reflecting a much lower-dimensional embedding. The patterns inherent in this mapping are "chunks" - which may be reified (become real) if they are encountered frequently. Eventually, if they acquire a label (a "phonological pole") they become a true symbol.
This process results in the emergence of rich, perceptually grounded symbols that are flexible and can infer many of the rules and behaviours that need to be painstakingly programmed in present computational knowledge systems.
We believe dimensionality reduction may be an important aspect of the discovery of chunks, which ultimately form the core of design symbols. In our preliminary work, we have found empirical evidence of such dimensionality reduction in many constrained-objective and multi-objective situations. The discovery of such patterns, often in an implicit manner, may also underlie the evolution of design expertise. Clearly, this is only a start and much further work is needed.In this research effort, we also investigate how these patterns of "good designs" may change with changes in embodiment or function, and also how these ideas may be applicable to problems such as product portfolio management.