Computer Networks (CS425)

In this lecture we will look at key exchange in symmetric key schemes where public key encryption cannot be used. So the encryption using public and private keys is not possible. We will see that in this scenario how do we exchange the symmetric key. The two people who are communicating do not want others to understand what they are talking about. So they would use a language which others possibly do not understand. But they have to decide upon a common language. For this the language has to be encrypted in some key which will be somehow known to the other person.

Key exchange in symmetric key schemes is a tricky business because anyone snooping on the exchange can get hold of the key if we are not careful and since there is no public-private key arrangement here, he can obtain full control over the communication. There are various approaches to the foolproof exchange of keys in these schemes. We look at one approach which is as follows:-

Diffie - Hellman Key Exchange

A and B are two persons wishing to communicate. Both of them generate a random number each, say x and y respectively. There is a function f which has no inverse. Now A sends f(x) to B and B sends f(y) to A. So now A knows x and f(y) and B knows y and f(x). There is another function g such that g(x,  f(y)) = g(y, f(x)). The key used by A is g(x, f(y)) and that used by B is g(y, f(x)). Both are actually same. The implementation of this approach is described below :

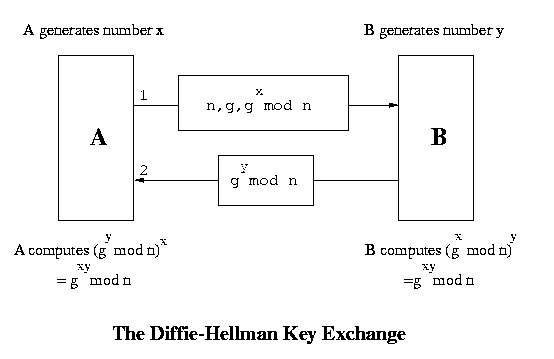
1. A has two large prime numbers n and g. There are other conditions also that these numbers must satisfy.
2. A sends n, g and g^x mod n to B in a message. B evaluates (g^x mod n)^y to be used as the key.
3. B sends g^y mod n to A. A evaluates (g^y mod n)^x to be used as the key. So now both parties have the common number g^xy mod n. This is the symmetric (secret communication) key used by both A and B now. 

This works because though the other people know n, g, g^x mod n, g^y mod n but still they cannot evaluate the key because they do not know either x or y.

Man in the Middle Attack

However there is a security problem even then. Though this system cannot be broken but it can be bypassed. The situation which we are referring to is called the man-in-the-middle attack. We assume that there is a guy C in between A and B. C has the ability to capture packets and create new packets. When A sends n, g and g^x mod n,  C captures them and sends n, g and g^z mod n to B. On receiving this B sends n, g and g^y mod n but again C captures these and sends n, g and g^z mod n to A. So A will use the key (g^z mod n)^x  and B will use the key (g^z mod n)^y  . Both these keys are known to C and so when a packet comes from A, C decrypts it using A's key and encrypts it in it's own key and then sends it to B. Again when a packet comes from B, it does a similar thing before sending the packet to A. So effectively there are two keys - one operating between A and C and the other between C and B.

There must be some solution to this problem. The solution can be such so that we may not be able to communicate further ( because our keys are different ) but atleast we can prevent C from looking at the data. We have to do something so that C cannot encrypt or decrypt the data. We use a policy that A only sends half a packet at a time. C cannot decrypt half a packet and so it is stuck. A sends the other half only when it receives a half-packet from B. C has two options when it receives half a packet :

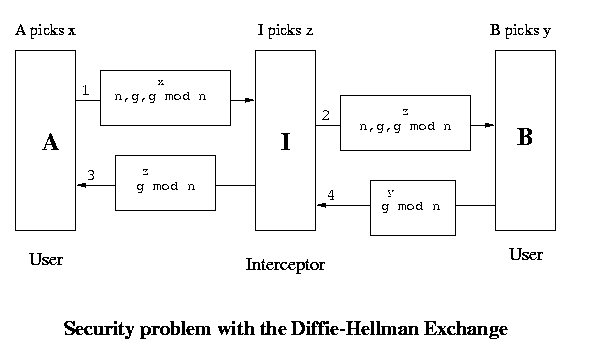
1. It does not send the packet to B at all and dumps it. In this case B will anyway come to know that there is some problem and so it will not send it's half-packet.
2. It forwards the half-packet as it is to B. Now when B sends it's half-packet, A sends the remaining half. When B decrypts this entire packet it sees that the data is junk and so it comes to know that there is some problem in communication.

Here we have assumed that there is some application level understanding between  A and B like the port number. If A sends a packet at port number 25 and receives a packet at port number 35, then it will come to know that there is some problem. At the very least we have ensured that C cannot read the packets though it can block the communication.

There is another much simpler method of exchanging keys which we now discuss :  

Key Distribution Center

There is a central trusted node called the Key Distribution Center ( KDC ). Every node has a key which is shared between it and the KDC. Since no one else knows A's secret key (K_A) KDC is sure that the message it received has come from A. We show the implementation through this diagram :

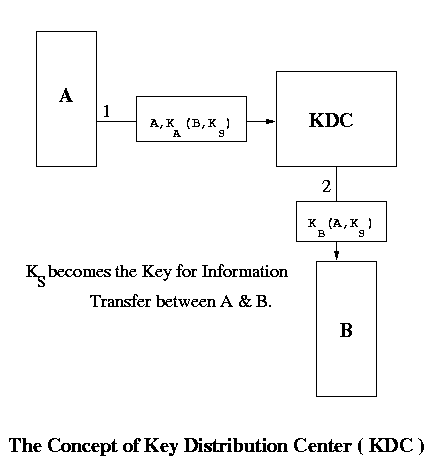
When A wants to communicate with B, it sends a message encrypted in it's key to the KDC. The KDC then sends a common key to both A and B encrypted in their respective keys. A and B can communicate safely using this key. There is a problem with this implementation also. It is prone to replay attack. The messages are in encrypted form and hence would not make sense to an intruder but they may be replayed to the listener again and again with the listener believing that the messages are from the correct source. To prevent this, we can use:

• Timestamps: which however don't generally work because of the offset in time between machines. Synchronization over the network becomes a problem.
• Nonce numbers: which are like ticket numbers. B accepts a message only if it has not seen this nonce number before.