LOCAL RULE-BASED PATH PLANNING METHODS
PRESENTATION BY
AKSHAY MOHAN 98023
LOCAL VS GLOBAL PATH PLANNING METHODS
GLOBAL METHODS: Try to capture the global connectivity of the robot's free space into a condensed graph that is subsequently searched for a path. They are based on searching procedures and could churn out paths that optimize the path length. The planning methodology involved further representation of the environment models in terms of suitable data structures such as graphs, trees so that finding a path in the workspace is equivalent to searching for a route between two nodes on the graph
LOCAL METHODS: The values and actions are not dependent on the distribution and shapes of the C-obstacles beyond some limited neighborhood of the current configuration/position of the robot. Real-time navigation strategies came up as a consequence of having to cope with pragmatic realities such as inaccuracy of environment models and the requirement of the robot to navigate in unknown and unstructured environments. These approaches generate a linear and angular speed during every sample instant as a combination of the response outputs for different behaviors such as obstacle avoidance and target reaching. The path generation is obtained by advancing the robot to a new position and by repeating the process.
NEED OF THE LOCAL METHODS
unknown environment
complexity, both in terms of implementability and time, of the algorithms that are global in nature
restrictions placed by the actual sensory devices present on a robot
CLASSICAL METHODS
potential field method
heuristic methods using fuzzy logic controllers
APPROACHES TO BE CONSIDERED PRESENTLY
1: Genetic Fuzzy Approach
2. Fuzzy Approach combined with perception and remembrance of the environment
GENETIC FUZZY APPROACH [1]
THE TECHNIQUE EXPLAINED
A genetic algorithm is used for developing an optimal fuzzy
logic controller. This effectively converts an online path planning problem to
an offline optimization problem. The
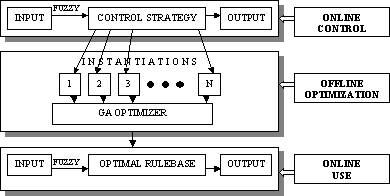
scheme is depicted in fig. 1.

Fig. 1. The GA-Fuzzy approach for robot motion planning
Instantiations of the control strategy to be implemented online are randomly generated and act as individuals for the GA population. The GA then optimizes the control strategy offline. The optimized rulebase as obtained by the GA is then used online for path navigation and obstacle avoidance. This allows the computationally intensive optimization to be done offline and leads to an efficient online implementation that gives an optimal path, yet which is able to do it in real-time and only using the scarce memory and computational resources available on an autonomous robot.
THE TECHNIQUE APPLIED TO PATH NAVIGATION
The
rules were represented as a set of condition-action pairs. The first condition
is the distance of the nearest obstacle forward from the robot. Here forward
means within the field of view of the robot. As our obstacles are square shaped,
the distance is calculated from the line joining the current position of the
robot to the point of intersection of line joining the robot to the center of
the obstacle and the nearest edge of the obstacle. The second condition is the
angle between the path joining the robot and the target point and the path from
the robot to the nearest obstacle forward. The action is represented by the
angle of deviation for the robot from the path joining the robot to the target
point. This is depicted in fig. 2.
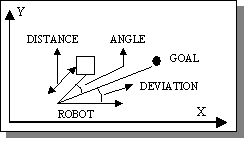
Fig. 2. The input (distance and angle) and output (deviation) variables of the fuzzy logic controller
Thus
angle and distance form the fuzzy inputs and deviation forms the output. Here
the fuzzy values for distance, angle and deviation are depicted in fig. 3.
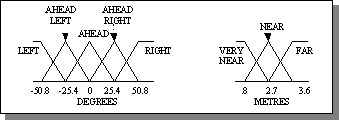
Fig. 3. The fuzzy membership functions for angle and deviation (left) and distance (right)
FITNESS EVALUATION
Triangular
membership functions were used with the relative spacing of the membership
distributions being constant. The membership functions were kept same for angle
and deviation.
RULEBASE
REDUCTION
The evolved
models of the optimal fuzzy logic controller (even the perfect individual) were
complicated and included a large number of rules that seemed redundant. The
evolved optimal rulebase for cases when the number of obstacles was changed to
8, 16, 32, 40, 64, 128 and 256 came out to be different. This should not be the
case as ultimately the final rulebase to be implemented on the robot would be
unique irrespective of the number of obstacles in the environment. After all if
one can know the number of obstacles in an environment, one can also know their
position and then the environment is no longer unknown!!
Local
search is performed on the optimal evolved rulebase that is able to solve all
the cases. Each of the possible subsets of the evolved rulebase is tested and
its fitness evaluated. Typically the rulebase consisted of seven to nine rules.
The
Rulebase Obtained
The
rulebase was evolved with a test-bed of 100 different cases. Each case has 40
obstacles of which 10 were placed on the path joining the start point of the
robot to the end point. Here the workspace was of size 80x80 with the initial
point being the origin and the goal point being (76,76). Goal was attained if
the robot came within unit distance from the goal.
The
GA evolved the perfect individual after 1581 fitness evaluations. The population
size of GA was kept 100, mutation probability 0.02 and crossover probability
0.9. Length of the string was kept 45 with the maximum number of allowed rules
in the rulebase being fifteen. The evolved rulebase is shown in table.1. Here
the first rule can be interpreted as: if the distance of the nearest obstacle
forward from the robot is very near and the angle between the line
joining the current robot position to the goal point and the line joining the
current robot position to the center of the obstacle is left, then the
robot should not deviate and go ahead.
Table 1. Perfect rulebase evolved by GA
|
Distance |
Angle |
Deviation |
|
Very near |
Left |
Ahead |
|
Very near |
Ahead left |
Ahead right |
|
Very near |
Ahead |
Right |
|
Very near |
Right |
Ahead left |
|
Near |
Left |
Right |
|
Near |
Ahead left |
Right |
|
Near |
Ahead |
Right |
|
Near |
Right |
Ahead right |
|
Far |
Ahead |
Right |
However
when we apply local search, the rule base is shortened to the one given in
table.2. This was due to the redundant rules that were present in the rulebase
evolved by the GA got eliminated by using local search. The number of rules in
the rulebase is reduced from nine to four without any reduction in the fitness.
Both of the rulebase are able to solve all the 100 cases in 11738 seconds, thus
taking on an average 117.38 seconds for each case as against the allowed maximum
time of 400 seconds.
Table 2. Perfect rulebase shortened by local search
|
Distance |
Angle |
Deviation |
|
Very near |
Right |
Ahead left |
|
Near |
Ahead left |
Right |
|
Near |
Right |
Ahead right |
|
Far |
Ahead |
Right |
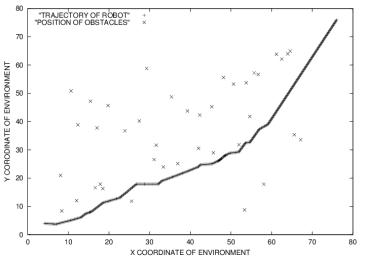
Fig. 4. The position of obstacles and the path of the robot obtained using the shortened rulebase
Thus we see that the robot is able to effectively navigate through obstacles and reach its goal. The path of the robot in the other ninety-nine cases is similar to the above curve and proves the efficacy of the technique.
FUZZY APPROACH COMBINED WITH PERCEPTION AND REMEMBRANCE OF THE ENVIRONMENT [2]
NEED
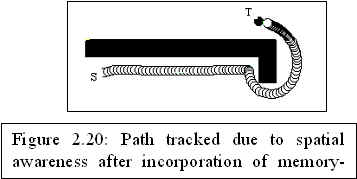
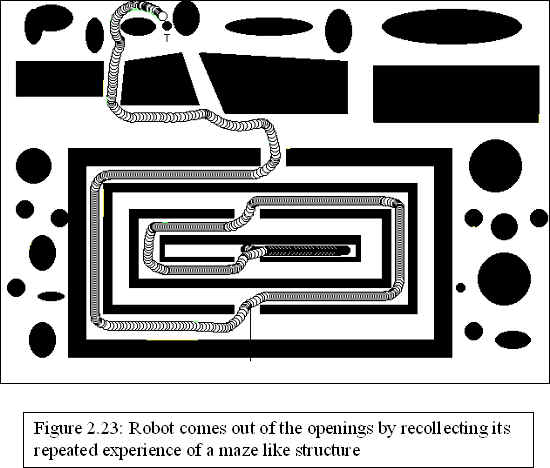
lack of memory-based behavior and reasoning is apparent in most of the algorithms and their absence become prominent during certain aspects of navigation like the robot's failure to get aware of local minimum traps.
ALGORITHM
IMPLEMENTATION
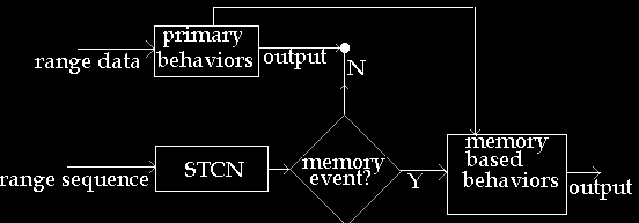
Fig5. The overall algorithm
BASIC BEHAVIOR
1. TARGET ORIENTING MODULE:
The input to the target orienting module is the difference angle mentioned in section 2.2. The output of the module is denoted as, or the turn angle of the robot (angle by which it must turn) due to the target reaching behavior. It is that behavior responsible for orienting the robot towards its target.
Input : Difference Angle
Output : Turn angle due to target
Rules : (i) If target is on the left then turn left (ii) If target is on the right then turn righ
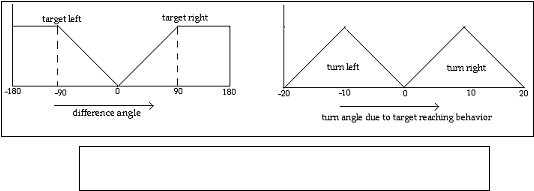
Fig 6. Fuzzy inference for target orientation
2.
Object
Avoidance Behavior Module:
Typical
rules of this module take the following linguistic form
1.
If the object is detected at near
ranges on the left then turn the robot right by a large
angle.
2.
If the object is detected at far
ranges on the left then turn the robot right by a small
angle.
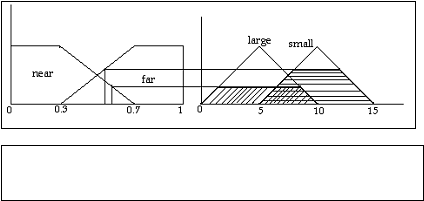
Fig 7. Fuzzy inference for object avoidance behavior due to sensor 6.
3. COBMINED BEHAVIOR
Hence the net change in orientation of the robot is considered as an weighted sum of the changes in orientation due to the individual modules. The weights ascribe the proportion of importance to the individual behaviors.
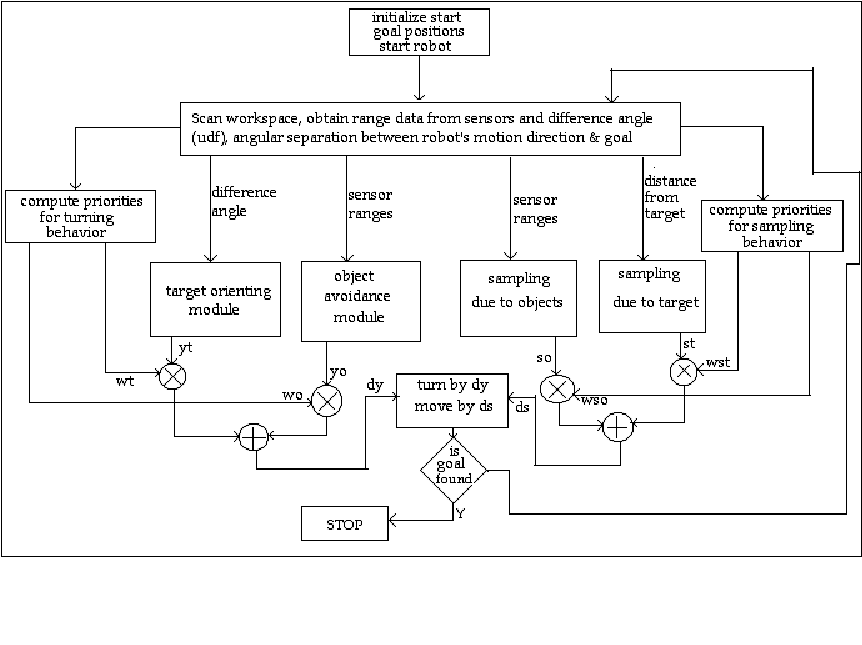
Fig 8. Flow diagram representation of real-time navigation with the primary modules alone
Adaptive fuzzy control where the parameters of the rulebase get tuned through a learning mechanism to obtain the desired performance or the desired input-output mapping through a network structure decides the parameters.

MEMORY MODULE

Fig:
Arrangement of sensors used in static environment
|
RIGHT
SENSOR |
CENTER
SENSOR |
LEFT
SENSOR |
CLASS |
|
VERY
NEAR |
VERY
NEAR |
VERY
NEAR |
0 |
|
NEAR |
NEAR |
NEAR |
1 |
|
NEAR |
NEAR |
FAR |
2 |
|
NEAR |
FAR |
NEAR |
3 |
|
NEAR |
FAR |
FAR |
4 |
|
FAR |
NEAR |
NEAR |
5 |
|
FAR |
NEAR |
FAR |
6 |
|
FAR |
FAR |
NEAR |
7 |
|
FAR |
FAR |
FAR |
8 |
Table
3:
Spatial classification of the range readings by Fuzzy rule base
A double layered network for spatio-temporal classification, which enables the robot to understand as well as remember the various scenarios encountered during its navigation is used. At the first layer fuzzy rule-base does the spatial classification and at the second layer SOM and Fuzzy ART network is used for temporal learning. The SOM captures to a reasonable accuracy the size and shape information of the obstacles or landmarks in the environment and provides stability to the network by accurate recall of previously stored patterns but is not plastic enough to new situations. The online classification property of Fuzzy ART however makes the network plastic to new patterns but its ability to interpret the environment is poor when compared to the SOM. Hence we use both the SOM and the ART in the second layer to avail the advantages of both.
A
navigating robot understands its environment in terms of landmarks. A landmark
such as a corridor can be considered as an experience of a temporal sequence of
sensory patterns and represented in terms of such spatio-temporal patterns.
Since remembering a moderately long traversal involves storing several instants
of sensory data resulting in huge memory requirements, a classification scheme
is essential for classifying the spatio-temporal data into meaningful
information. The spatio-temporal classifier network does this.
In the proposed scheme spatial understanding is achieved through the weight vectors of the neurons that are codified representations of the local space of the robot. Storing the lattice positions of the winning neurons during a traversal enable storage of the comprehended scenarios while choosing a particular lattice position achieves focussing on a particular remembered experience. And temporal correlation of a particular experience occurs through recall when the neuron coding that experience gets activated more than once during traversal.
A
landmark is modeled as an experience of spatio-temporal patterns. Each sample of
such a pattern consists of range readings obtained by the seven sensors. For
reducing complexity of storage, representation and learning a long sequence of
such samples, each sample is mapped to a class by the fuzzy classifier. The
number of such classes in a temporal sequence is fixed at 3 with no two
consecutive classes being identical. The minimum number of times each class must
occur in a sequence to filter noisy samples is termed the lower bound for that
class. The structure of the double layered classifier network is shown in figure
9.
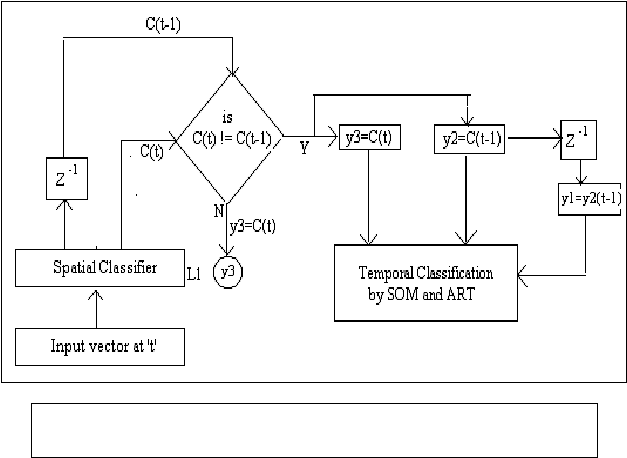
Fig
9. Structure
of the spatio-temporal classifier network
The
structure represents the process of extracting the temporal order of the classes
before giving it to the second layer. As discussed in the previous paragraph any
two consecutive classes in the final sequence to be classified must be
different. The comparator (figure 2.16) which compares the present class C(t)
with the class of the previous instant C(t-1) does this. When the compared
values are different C(t-1) is extracted to form the first class in the sequence
to be classified by the second layer. The process is repeated and when three
such classes are extracted the sequence, y1, y2, y3 (see figure 2.16) is input
to the second layer of the classifier.
Consolidated understanding of the environment is that spatial understanding derived by considering a sequence of preliminary spatial understandings ordered in time. . The sequences are obtained by navigating the robot across landmarks typically encountered in indoor environments. These sequences are reduced to a sequence of 3 classes and presented as inputs to be learned by the temporal classifier (fig 9). The SOM is trained over these sequences of classes. On encountering a sequence of patterns that represents a particular landmark the neuron in the lattice is triggered and the robot becomes aware or cognizant of the presence of such a landmark in its vicinity.
Fuzzy ART is capable of learning new patterns and simultaneously remembers the earlier patterns to a reasonable accuracy. It eliminates the need for maintaining a map of large neurons most of which are idle. The ART network can dynamically add new patterns according to the local environment of the robot and can afford to forget patterns that have not come within a recent time interval, say in the last hundred samples of the environment thus memorizing the environment to the extent needed.
.
As the robot navigates through the environment the sensory inputs are obtained
and classified by the first layer of the classifier network. The temporal order
of classes is extracted. A sequence of 3 such classes with no two consecutive
classes being identical forms the input vector for the Fuzzy ART. The Fuzzy ART
maps the sequence with an earlier one or adds a new spatio-temporal pattern to
the existing set of patterns. The decision for adding a new pattern is decided
by the vigilance parameter, which is set to 0.9 in our algorithm. A review of
the Fuzzy ART algorithm had been given in the previous section.

References
1. Pratihar, D.K.: Path and Gait Generation of Legged Robots Using GA-Fuzzy Approach. PhD Disseration, Department of Mechanical Engineering, Indian Institute of Technology – Kanpur, May 1999 (1999).
2. Krishna, K. Madhava: Soft Computing Applications to Real-time Navigation of a Mobile Robot in Stationary and Dynamic Environments. PhD Disseration, Department of Mechanical Engineering, Indian Institute of Technology – Kanpur.