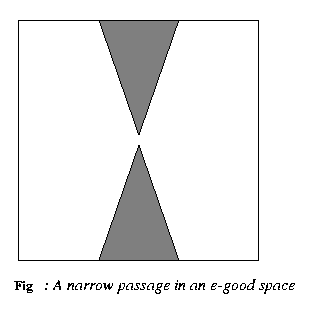Probabilistic Roadmap Methods
Motivation:
Probabilistic roadmap methods have proved to be very effective for path
planning in high dimension configuration spaces. Typically, complete planners
require time exponential in the dimension of C-Space. For robots with greater
than 5 dofs, these methods become practically useless.
Randomized Path Planners(RPP), which use random walks to escape local
minima, have been found to be effective in many practical cases. However,
there are a number of pathological cases where they badly fail. These are
cases where the only way to escape a local minima is a narrow passage.
The random walk is often not able to find the narrow passage.
PRM however has been found to be effective for robots with upto 15
dofs. The typical number of obstacles is of the order of tens of thousands
of polygons.
In this lecture, we shall discuss some of the implementation issues
involved in path planning using PRM
Basic PRM Technique:
PRM consists of two phases:
Preprocessing phase
Query processing phase
Preprocessing phase:
-
Randomly select s 'milestones' from F, the free space
-
Generate roadmap R by trying to connect every pair of milestones.
Query processing phase:
-
Try to connect both qstart and qgoal
to
some milestones mi and mj in the roadmap
R.
-
If there is a path from mi to mj
in
the roadmap R, output the path, else return failure.
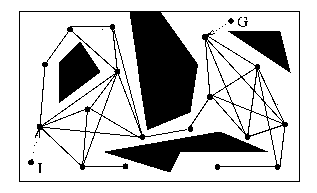
The following figure shows a roadmap constructed for a space with
polygonal obstacles.
Practical implementations use some variations in the above scheme:
-
Instead of connecting every pair of milestones in step 2 of preprocessing,
try to connect only those pairs which lie in a 'neighbourhood' of each
other.
-
Instead of randomly selecting the milestones, select them in an expanding
tree fashion. i.e build expanding search trees from both qstart
and
qgoal
till the two trees intersect.
-
Instead of checking the path connecting two milestones for collision in
the processing phase, delay it till the actual path has been found. Do
the collision checking only for milestones lying on the path.
Implementation Issues :
The set of milestones generated must be 'good'. That is, it should satisfy
the following criteria:
-
Any configuration q should be able to connect to some milestone
mi
of
the roadmap
-
The connectivity obtained by the roadmap should accurately reflect the
actual C-space connectivity i.e two components of the roadmap should be
connected whenever there exists a path between the two in the C-Space.
For generating a good set of milestones, the following two factors are
critical:
-
Number of milestones
-
How new milestones are selected
Empirically it has been found that for a good roadmap, there should be
a milestone in every d-neighbourhood of a milestone. d is typically 0.1
- 0.3 of the length of a dimension.
Theoretical justification:
Exact bound on the number of milestones required are difficult
to find because of the difficulty of exactly characterizing the C-Space.
There have been some attempts to characterize the goodness of the C-Space
which we discuss below:
Visibility Assumption - e goodness:
e-goodness
of a space can be thought of the minimum visibility of the space. A point
p
in C-Space is said to be e-good if it can see at least an e
fraction of the free space F. The e-goodness of the entire space
is the e-godness of the point in the space with least e-goodness.
Below is an example showing
a space which is not e-good for any e.

Visibility Assumption - Roadmap connectedness
For roadmap connectedness, we
define the notion of expansiveness. Thsi is directly related to the difficulty
that roadmap has to connect milestones through narrow passages. Basically,
expansiveness is a measure of how much a set of milestones can expand to
generate new milestones. A space might be e-good, but can have poor
expansiveness as illustrated in the following figure.
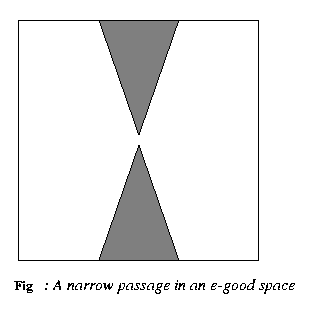
Theoretical analysis based on the above characterizations of C-Space
yield the result that probability of failure decreases exponentially with
the number of milestones.
Narrow passages:
Though PRM has been found to be very efficient for most practical cases,
it fails badly in some cases. These are the cases when the required path
passes through a narrow passage. The probability of generating milestones
in the narrow passage by purely random sampling is very low. We will discuss
some techniques to improve the conectivity of the roadmap. These techniques
basically try to generate milestones near the boundary of the free space.
The following figure shows a C-Space with an narrow passage in
it.
Resampling techniques:
Suppose N is the number of milestones
generated by the preprocessing stage. We generate M additional milestones
(M ~ N/2) where the connectivity needs to be improved.
The new milestone is randomly
sampled from the neighbourhood of an existing milestone mi .
mi
is chosen as follows. For each milestone mi let
bidenote the number of milestones to which it was successfully
connected. Then, probability that mi is selected
is proportional to 1/(bi +1)
For details refer [1]
Ray shooting-based techniques:
These techniques generate points
near the boundary of the C-Space by searching along a ray in random
direction. Details below:
1. When a milestone
mi
is found to be outside free space F, a number of rays are shot from
mi along random directions uniformly distributed in C-Space.
For each ray, a binary search is used to identify a point near the boundary
of F.
For details refer [2]
2. A single ray is shot from
mi,
a milestone outside F, along a random direction; the procedure then
simulates a walk of the robot in this direction, until it reaches free
space.
For details refer
[3]
3. A ray is shot from a milestone
in one component along a direction picked at random. A milestone is created
when this ray encounters the free space boundary and the ray is reflected
in a random direction at this point to find another boundary point.
For details refer [4]
New-Roadmap Technique:
This new roadmap-construction
algorithm starts starts by constructing a roadmap R' in a dilated
space F' obtained by allowing some penetration distance d of the
robot into the obstacles. Next, it "pushes" the milestones and links of
R'
that do not lie in F into F by preforming local resampling
operations. The outcome is a roadmap R in F. The rationale
behind this two-stage strategy is that free space dilation widens narrow
passages and thus makes it easier to capture free space connectivity.
The following figure illustrates the operations
of the algorithm:

A formal description of the algorithm is given below:
procedure new-roadmap:
1. Generate a roadmap
R'
= (M', L') of size s' in the dilated free space F'
by invoking roadmap.
2. Initiate a roadmap
R
= (M, L) in the free space F by setting M and
L to the empty set.
3. for each
milestone m in M' do:
(a) if m lies in F then add m
to M
(b) else repeat x times:
i. Pick a configuration q uniformly at random in Um(m).
ii. if q lies in F then add q
to M.
(c) if a configuration has been added to M at any of
the above steps, then denote this configuration by p(m)
4. for each link (m,
m')
in L' do:
(a) if p(m) sees p(m') then add (p(m),
p(m'))
to L.
(b) else
i. Pick y configurations uniformly at random in Ul(p(m),
p(m')). Let Q be the subset of those configurations which are
in F.
ii. if there exists a sequence q1, ...,
qk of configurations in Q, such that p(m)
sees
q1, qi sees qi+1 for
i = 1, ..., k-1, and qk sees p(m'),
then:
. Add every qi, i = 1, ..., k
to M.
. Add every (qi, qi+1), i
= 0, ..., k-1 to L.
Results using this algorithm:
The following diagrams show
the set of milestones generated using roadmap versus new-roadmap algorithm.
Clearly, the new algorithm finds more milestones in the narrow passages.

References:
[1]: L. Kavraki, P. Svestka, J.C. Latombe, and M. Overmars Probabilistic
Roadmaps for Path Planning in High-Dimensional Configuration Spaces. IEEE
Tr. Rob. and Aut., 12(4):566-580, 1996
Get Paper
[2]: N. Amato and Y. Wu A Randomized Roadmap fro path and Manipulation
Planning. Proc. IEEE Int. Conf. on Rob. and Aut., Minneapolis, MN,
pp.3303-3308, 1996.
Get paper
[3]: M. Overmars. A random Approach to Motion Planning. Tech. Rep. RUU-CS-92-32,
Comp. Sc. Dept., TB Utrecht, The Netherlands, 1992
[4]: T. Horsch, F. Schwartz, and H. Tolle. Motion Planning for Many
Degrees of Freedom - random Reflections at C-Space Obstacles. Proc.
IEEE Int. Conf. on Rob. and Aut.,San Diego, CA, pp. 3318-3323, 1994