Ashish Agarwal, Mayank Agrawal
IIT Kanpur : February 2000
Contents
Motivation Example: Some-Sample-Task Past Work Methodology Results Implementation Details Conclusion Bibliography
Motivation
Plane geometry is a classical field of mathematics rich in beautiful and elegant theorems. The proofs of many of these theorems are challenging as they require a reasonable amount of ingenuity and deductive reasoning. Generating formal proofs is considered to be an intelligent task guided by intuition. It is appealing to think if a computer program capable of proving geometric theorems can be made.Such a program has a high theoretical value as it can help mathematicians to explore and prove new theorems. It can also be an educational tool as it can help students by explaining them step by step solutions to problems.
The task of the program is to take in the hypothesis and conjecture of a problem. It analyses the given hypothesis and automatically generates the diagram relevant to the problem. The diagram generated is different each time and gives insight into the various order relationships that can hold for a given set of hypothesis. It than proceeds to generate the proof if the conjecture is true. The problems can be of varied nature from plane Euclid geometry.
(back to the top )
Example :
Problem:
Prove that the centroid of a triangle divides the
median in the ratio 2:1
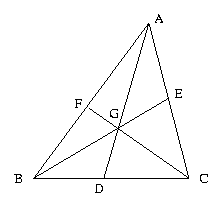
Machine Input:
Points: A, B, C, D, E, F, G
Hypothesis: mid(E,A,C), mid(D,B,C),
mid(F,A,B)
collinear(B,G,E), collinear(C,G,F),collinear(A,G,D)
Conclusion: GD/AG=1/2
Machine Output:
Proof: GD/AG
= -GD/GA
( Canonized form )
= [EDB] / [EBA]
( L5: because collinear(A,G,D), collinear(B,G,E) )
= ( [ECB] (DB/CB) ) / ( [CBA] (EA/CA) )
( L4: because collinear(D,B,C), collinear(E,A,C) )
= ( [ECB] (1/2) ) / ( [CBA] (1/2) )
( because mid(D,B,C), mid(E,A,C) )
= ( [ECB] ) / ( [CBA] )
( simplification )
= ( [CBA] (EC/CA) ) / ( [CBA] )
( L5: because collinear(E,A,C) )
= 1/2
( simplification )
Such and many other problems can be tackled by the program. The program will generate step by step proof with proper justification.
(back to the top )
Past Work
[Gelernter:1963] : The initial work was done by Gelernter. His program relied on congruency of triangles. He used backward chaining to create (AND/OR) tree of goals and subgoals. He also used numerical information from a sample diagram to eliminate unrealistic goals. Search space explosion limited the application of his method to only some High school level geometry problems.[Nevins:1975] : He also used congruency of triangles as a fundamental result. He emphasized on the use of forward chaining.He maintained a data base of known results and used the information present to derive new results.The user had to specify the exact order relationships existing in the diagrams.His method did not deal with circles or proportionalities.
[Wu:1978] : Because of the inability of synthetic methods to tackle difficult problems, focus shifted to algebraic methods. Wu used a method where the hypothesis and conclusion statements of a problem were translated into algebraic relations.User had to specify constructibility order of the points. Based on this order, the variables (coordinates of points) were classified as independent and dependent. The hypothesis relations were then transformed to a standard triangulated form and the dependency of the conclusion on the hypothesis was checked.
[Chou:1988] : Chou implemented Wu's method to build a theorem prover. It was capable of proving many difficult geometry problems. But this ability was gained at the expense of elegance. The proof now consisted of complex algebraic manipulations and was not worth reading.
[Chou/Gao/Zhang:1996] : They have addressed the problem of generating human readable proofs. They introduced the concept of using some geometric invariants such as the signed area of triangle, the ratio of directed segments and full angle for this purpose. Backward chaining was mainly used for proving the conjectures. The proofs were elegant, short and independent of the order relationships of points. The need of auxiliary constructions was also minimized.
We have used the concept of area and full angle,
as suggested above.We have selected a set of lemmas and a set of
predicates suitable for proving a large class of problems. We are using
backward chaining as the main deduction technique. To reduce the search
space and to improve efficiency, some amount of forward chaining is also
employed. The idea of the constructibility order of points has been used
to direct the search.
(back to the top )
The first task of the program is to generate the diagram
of the problem. We take as input from the user the points and the hypothesis
predicates. We assign coordinates to each of the points, and then each
hypothesis predicate is translated into an algebraic relation.
eg. if given points A,B,C,D and perp(AB,CD) then
-
Let A=(x1,y1) B=(x2,y2) C=(x3,y3) D=(x4,y4)
Now perp(AB,CD) implies that the product of slopes of AB & CD is
-1;
(y2-y1) (y4-y3) + (x2-x1) (y4-3) = 0
We thus generate a list of polynomial equations representing the constraints of problem. We then divide the variables in sets of independents and dependents. Random values are chosen for the independent variables and the values for dependent variables are solved. Each time this program generates a different diagram and can illustrate various possible order relationships that can exist for any given problem statement.
We have used the area method and the full angle method for proving.The strategy used is backward chaining.Area here represents the signed area, positive for the anticlockwise orientation of points, and is represented as the triplet of points. eg. [ABC] .Full angle between two lines represents the amount of anticlockwise rotation necessary to make one line parallel to the other.It is represented by the endpoints of the line segments. eg.[AB,CD]
The problem is specified by specifying the points
and the relationships between the components like points, lines, segments,
angles,etc. A collection of commonly used predicates
has been selected to be able to represent most of the problems.Some of
the predicates used are as follows:-
collinear, parallel, perpendicular, midpoint, congruent
(for segments), eqangle (two angles equal),etc.
The problem is specified by listing the points followed by the relations in terms of the predicates.The conclusion is specified either as an expression involving the invariants or in terms of some predicate.
The prover uses backward chaining to derive the proof. A set of lemmas has been built into the program. The lemmas are in terms of an algebraic relationship among the invariants when certain relations are true.The conclusion statement is converted into an equality involving polynomials in the invariants. The prover tries to prove this equality by making replacements in the expressions using the lemmas and simplifying the resulting expressions. For this, a complete symbolic manupulation routine has been inbuilt into the program.
Example:
Consider the problem of proving that the centroid
divides the median in the ratio 2:1.
At the beginning, the program has a database of six predicate relations and the conclusion expression (GD/AG).It first converts all the invariants (terms of area, ratio of segments) to a cannonical form. This is done to avoid unnecessary search involving different permutations of the same term.
The prover checks all the lemmas to see if any of them can be applied.If the requirements are satisfied, it makes the replacement and simplifies the resulting expression. In this case, it finds that it can replace the ratio of segments by the ratio of area by applying lemma 5. So it goes on to make the replacement and then tries to carry the same procedure on the resulting expression. Everytime the search fails, the program backtracks. If it fails to prove the conclusion, it quits and indicates the failure to the user. In this case, the program succeeds in finding a proof by the above procedure.
The process has been modelled as a graph search, where the nodes represent the current state of the expression and the application of the lemmas, the edges. Iteratively deepening depth first search is used to search for the proof. This guarantees the generation of the shortest proof if one exists.
An important concept that has been utilized is the constructibity order among the points. The class of constructible problems (those in which points can be successively obtained from the previous points only by simple constructions like taking intersection of circles, lines, etc, or by taking the point arbitrarily) permit of an ordering among the points. This can be useful because, in general, the proof for this class can be got by eliminating points of higher order.
We are taking the ordering of points from the user. This order has been used as a search heuristic for making the search directed by giving a higher preference to elimination of points of higher order.At each step of replacement, a higher priority is given to those lemmas which involve points of lower order.
The full angle method follows exactly the same procedure as the area method except for one difference - in addition to the strategy of backward chaining, it uses forward chaining as well.This is done to improve the efficiency of the prover and to decrease the length of the proofs. The full angle method relies heavily on the relationships among angles. So forward chaining is used to discover new circles and to find new parallelity or perpendicularity relations if possible. However, the forward search is done only to a very limited extent as it is generally costly in terms of time and space.
We have used the concept of area and full angle, as suggested above.We have selected a set of lemmas and a set of predicates suitable for proving a large class of problems. We are using backward chaining to deduce the results.To reduce the search space and to improve efficiency, we have used forward chaining,but only to a limited extent. The idea of the constructibility order of points has been used to direct the search.
(back to the top )
Results
The prover was able to prove a large number of
problems ranging from simple ones to those of fair complexity, some
of which are listed below. The proofs generated were short and elegant.
Some of them were, infact, quite similar to the traditional proofs.
One problem that occured in the generation of proofs
was that of search space explosion. Several control strategies were employed
to control the growth of search space. The most important being the one
using constructibilty order of points. But the control strategies involved
a tradeoff. Although they were effective in checking the size of search
space, they sometimes also resulted in restricting the search for a proof.
After completing the basic framework of program
we tried several versions of control strategies. A general control strategy
was difficult to find as different strategies gave better results for different
problems. To increase its capability, we also built a one step look ahead
strategy, so that if the resulting expressions though in conflict with
the control strategies at present, if can be simplified in the next step,
were carried through.
Except for a few cases, most of the proofs were
generated surprisingly fast, sometimes in less than a second ! Some of
these problems we ourselves were unable to prove.
We have a sample of proofs generated by our prover ( The diagrams here are also generates by our program) :-
1. Ceva's Theorem
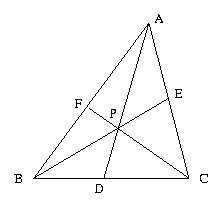
Point order: A,B,C,P,D,E,F
Hypothesis: collinear(A,F,B), collinear(C,P,F), collinear(B,D,C),
collinear(A,P,D), collinear(C,E,A), collinear(B,P,E)
Conclusion: (AF/FB)(BD/DC)(CE/EA) = 1
Proof: (AF/FB)(BD/DC)(CE/EA)
( canonization )
= -(EC/EA) / ( (FB/FA)(DC/DB) )
( L5: because collinear(A,C,E), collinear(B,E,P) )
= ( [PCB] [PCA] ) / ( (DC/DB) [PCB] [PBA] )
( simplification )
= ( [PCA] ) / ( (DC/DB) [PBA] )
( L5: because collinear(B,C,D), collinear(A,D,P) )
= ( [PCA] [PBA] ) / ( [PCA] [PBA] )
( simplification )
= 1
2. Pascal's Theorem
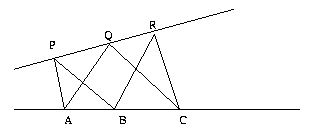
Point Order: A, B, P, Q, C, R
Hypothesis: collinear(A,B,C), collinear(P,Q,R),
para(A,Q,B,R), para(B,P,C,Q)
Conclusion: para(C,R,A,P)
Proof: para(C,R,A,P) <=> [CAP]=[RAP]
( [CAP] ) / ( [RAP] )
( canonization )
= ( [CPA] ) / ( [RPA] )
( L3: breaking area into sums )
= ( [CPB] + [CBA] - [PBA] ) / ( [RPQ] + [RQA] + [QPA] )
( L1: because collinear(A,B,C), collinear(P,Q,R) )
= ( [CPB] - [PBA] ) / ( [RQA] + [QPA] )
( L2: because para(B,P,C,Q), para(A,Q,B,R) )
= ( [QPB] - [PBA] ) / ( -[QBA] + [QPA] )
( L3: breaking area into sums )
= ( [QPA] - [QBA] + [APB] - [PBA] ) / ( -[QBA] + [QPA] )
( simplification )
= ( [QPA] - [QBA] ) / ( -[QBA] + [QPA] )
( simplification )
= 1
3. Simson's Theorem
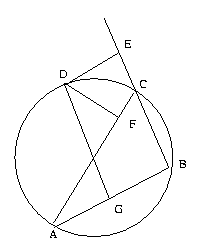
Point Order : A, B, C, D, E, F, G
Hypothesis : cyclic(A,B,C,D),
perp(D,E,B,C), perp(D,F,A,C), perp(D,G,A,B),
collinear(B,C,E), collinear(C,A,F), collinear(A,B,G)
Conclusion : collinear(E,F,G)
Proof : collinear(E,F,G) <=> [GF,GE]=0
[GF,GE]
( L9: breaking the angle into sums )
= [GF,GD] + [GD,GE]
( L6: because cyclic(F,G,D,A), cyclic(E,G,D,B) )
= [FA,DA] - [EB,DB]
( L3: because collinear(A,C,F) )
= -[DA,CA] - [EB,DB]
( L3,L6: because collinear(B,C,E), cyclic(B,C,D,A))
= -[DA,CA] + [DA,CA]
( simplification )
= 0
4. Miquel Point Theorem
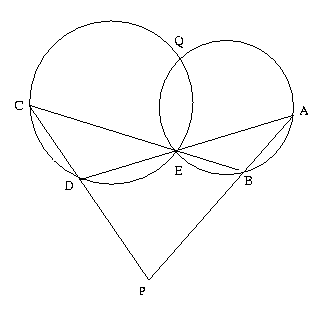
Point Order : A, B, C, D, E, Q, P
Hypothesis : cyclic(A,B,E,Q), cyclic(C,D,E,Q),
collinear(A,B,P), collinear(C,D,P),
collinear(B,C,E), collinear(A,D,E)
Conclusion : cyclic(D,A,P,Q)
Proof : cyclic(D,A,P,Q) <=> [PD,PA] - [QD,QA]=0
[PD,PA] - [QD,QA]
( L3: because collinear(C,D,P), collineaar(A,B,P) )
= -[QD,QA] + [DC,BA]
( L9: breaking the angle into sums )
= -[EC,DC] + [EB,BA]
( L6: because cyclic(D,Q,E,C), cyclic(A,Q,E,B) )
= [EC,DC] - [EB,BA] + [DC,BA]
( L9: because collinear(B,C,E) )
= [EC,DC] - [EB,BA] + [EB,BA] - [EC,DC]
( simplification )
= 0
( see the list of problems
for the proofs generated by the prover )
(back to the top )
Implementation Details
The prover is implemented in java. The program consists of three main segments. The first one for generating diagrams and the other two for Area Method and Full Angle Method. There is also a set of routines for symbolic manipulations. A main controlling program is there which interacts with the user and calls the appropriate routines.The diagram segment consists of an object called diagram. Functions are provided to deal with the insertion of predicates, and then to display the diagram. A new window frame containing the diagram is displayed on the screen.
The symbolic manipulation part consists of objects Expression, Term, ProductList, and Rational Expression. Functions are provided for the algebraic manipulations of these quantities.
The area method consists of an object AreaSolver . The functions provided deal with the insertion of the predicate, and the calling of iterated depth first search to find the proof.
The full angle segment consists of an object fangle.
An instance of this object represents the specific problem. The object
has a large number of functions for
external use which are called by our interface program. These functions
mainly deal with the insertion of new predicates for the specific function,
checking whether some predicate is true (using the forward chaining data
base) and the idfs function for starting iterated depth first search with
appropriate parameters.
(back to the top )
Conclusion
This program using area and full angle method is able to prove several non-trivial geometry theorems. Its strength lies in proving problems of constructive type where many theorems are very difficult for humans to prove. We were able to find short proofs of some theorems which we ourselves were not able to prove. The method however is not complete, and in general case we cannot verify the truth of conjecture.A major drawback with the present work is that the area method and full angle method work indepently of each other. Therefore it is weak for problems which require both angle and ratio relationships. An important further work can be to combine the two methods. The resulting method will be obviously more robust and would be able to deal with a larger class of problems.
The method used by us do not make use of similarity or congruency of triangles. Proofs generated by these methods look more mechanical, whereas the proofs by congruency and similarity are more elegant. Humans generally use congruency and similarity to generate proofs. Therefore an interesting extension of the present work can be to use congruency and similarity of triangles to generate more elegant and human like proofs.
(back to the top )
Bibliography
@Book{Chou:1988,
author= { Chou S.C.},
year= { 1988},
institution={ Mathematics Dep., Texas University, Austin},
title= { Mechanical Geometry Theorem Proving},
annote= {
This book describes a geometry theorem prover program
based on Wu's method. Part I of the book deals with the
mathematical theory and implementation of method. Part II
contains an appendix of over 400 theorems which have been
proved by this program. Most of these theorems are non-
trivial and illustrate the strength of this method. The
proofs are however fully algebraic and are not provided.
- Ashish Agarwal 10/2/2K },
}
@InCollection{Gelernter:1963,
author= { Gelernter H.},
year= { 1963},
title= { Realisation of a geometry theorem proving
machine},
book= { Computers and Thought},
pages= { 134-152},
annote= {
This paper is the very first attempt to proving
geometric theorems. The author has described a simple
deductive scheme. Search for the proof is mainly done
through backward chaining by creating a tree of goals and
subgoals. Being the very first attempt, the prover is
limited in scope and the author is content with proving
some high school level geometry problems.
- Mayank Agrawal 10/2/2K },
}
@Article{Nevins:1975,
author= { Nevins Arthur J.},
year= { 1975},
institution={ AI lab, MIT, USA},
title= { Plane geometry theorem proving using forward
chaining }
journal= { Artificial Intelligence},
volume= { 6},
number= { 1},
pages= { 1-23},
annote= {
A deductive scheme relying on forward chaining is
described. The author has emphasized over the importance of
forward chaining as the main tool, though backward chaining
is also employed. Some schemes are suggested to take into
account the order of points lying in the plane. Problem
domain is restricted to straight lines with no
proportionality relations.
- Mayank Agrawal 10/2/2K },
}
@InCollection{Wu:1978,
author= { Wu Wen-Tsun},
year= { 1978},
institution={ Institute of Systems-Sciences, Academica
Sinica, Beijing},
title= { On the decision problem and the mechanization
of theorem proving in elementary geometry},
book= { Automated Theorem Proving: After 25 Years},
pages= { 159-172},
annote= {
An algebraic approach for proving geometry theorems is
introduced. The given hypothesis and conjecture of a
problem are translated into polynomial equations and some
algebraic manipulations are done to see if these are
consistent or not. The method can be applied to several
domains of geometry and can prove many non-trivial
theorems (difficult for humans to prove).
- Ashish Agarwal 10/2/2K },
}
@Article{Chou/Gao/Zhang:1996,
author= { Shang-Ching Chou and Xiao-Shan Gao
and Jing-Zhong Zhang},
year= { 1996},
keywords= { automated reasoning, automated geometry theorem
proving, forward chaining, backward chaining},
institution={ Department of Computer Science, Wichita State
University, Wichita, USA},
title= { Automated Generation of Readable Proofs with
Geometry Invariants},
journal= { Journal of Automated Reasoning},
volume= { 17},
pages= { 325-369},
e-mail= { chou@cs.twsu.edu,gao@cs.twsu.edu,
zhang@cs.twsu.edu},
annote= {
This paper addresses the problem of generating human readable
proofs of geometry theorems. Authors have introduced two methods-
Area method and Full-Angle method to solve the problems. The main
advantages with these methods are :-
1. Can prove difficult theorems without the need of auxiliary
constructions.
2. Can produce diagram independent proofs, as they don't rely on
order relationships of points.
The authors have selected a set of lemmas for these methods which
can be applied to solve a large class of problems. They have
described a backward chaining search strategy to find the proof.
They have also suggested some control strategies to restrict the
search space. The results show quite a few difficult theorems
proved by their method.
- Mayank Agrawal 4/4/2K },
}
(back to the top )
[ COURSE WEB PAGE ] [ COURSE PROJECTS 2000 (local CC users) ]