topics: |  math | puzzle |

Kordemsky's Matematicheskaya Smekalka (1954) is probably the world's best-selling book of mathematical puzzles, with more than a million copies sold in the Soviet Union, and many more in translation. It was late in being translated into English (1972), and the translation replaces Kordemsky's original introduction with a short note from Gardener.

The puzzles are simple, and illustrations work well. However, the text is sometimes a bit cryptic - e.g. see my comment below puzzle 3.

Like most compilations, many puzzles are from other sources, but a significant fraction is original. The puzzles vary in their level of challenge (as the sampling below shows).

Kordemsky playing with 3-D puzzles.
photo by Anatoly Kalinin, from ageofpuzzles.com

About the title - why 359?  It's a prime.
But the original text by Kordemsky had more puzzles - especially on 
number theory.  Gardener pruned these since he felt these would require more
specialized knowledge. 

Excerpts

from Intro by Martin Gardener

This is the first English translation of Mathematical Know-how, the best
and most popular puzzle book ever published in the Soviet Union. Since its
first appearance in 1956 there have been eight editions, as well as
translations from the original Russian into Ukrainian, Estonian, Lettish,
and Lithuanian. Almost a million copies of the Russian version alone have
been sold.  Outside the U.S.S.R. the book has been published in Bulgaria,
Rumania, Hungary, Czechoslovakia, Poland, Germany, France, China, Japan,
and Korea.

The author, Boris A. Kordemsky, who was born in 1907 [d.1999], is a talented
high school mathematics teacher in Moscow. His first book on recreational
mathematics, The Wonderful Square, a delightful discussion of curious
properties of the ordinary geometric square, was published in Russian in
1952. In 1958 his Essays on Challenging Mathematical Problems appeared. In
collaboration with an engineer he produced a picture book for children,
Geometry Aids Arithmetic (1960), which by lavish use of color overlays, shows
how simple diagrams and graphs can be used in solving arithmetic
problems. His Foundations of the Theory of Probabilities appeared in 1964,
and in 1967 he collaborated on a textbook about vector algebra and analytic
geometry. But it is for his mammoth puzzle collection that Kordemsky is best
known in the Soviet Union, and rightly so, for it is a marvelously varied
assortment of brain teasers.

from biography by Will Shortz and Serhiy Grabarchuk

http://www.ageofpuzzles.com/Masters/BorisKordemsky/BorisKordemsky.htm

Boris Kordemsky (1907-1999), a Russian teacher and popularizer of
recreational mathematics, is probably the best-selling author of nonword
puzzle books in the history of the world. Just one of his books,
Matematicheskaya Smekalka (or, Mathematical Quick-Wits), sold more than a
million copies in the Soviet Union/Russia alone, and it has been translated
into many languages. By exciting millions of people in mathematical problems
over five decades, he influenced generations of solvers both at home and
abroad.

Knowledgable solvers recognized some of the puzzles as the original
inventions of the American Sam Loyd, the British Henry E. Dudeney, the
Belgian Maurice Kraitchik, and others. But undoubtedly a significant number
of the puzzles were new.

[this page also has four puzzles]

Puzzles

3. Moving Checkers

Place 6 checkers on a table in a row, alternating them black, white, black,
white, and so on, as shown. [e=empty; B=black, W=white]

		. . . . B W B W B W

Leave a vacant place large enough for 4 checkers on the left.

Move the checkers so that all the white ones will end on the left, followed
by all the black ones. The checkers must be moved in pairs, taking 2 adjacent
checkers at a time, without disturbing their order, and sliding them to a
vacant place. To solve this problem, only three such moves are necessary.

[The phrase "slide them to a vacant place" gives the impression (to me) that
one should slide it along the line.  A little observation however shows
that this cannot result in a solution. ]

4. Three Matchstick piles

Place three piles of matches on a table, one with 11 matches, the second with
7, and the third with 6. You are to move matches so that each pile holds 8
matches.  You may add to any pile only as many matches as it already
contains, and all the matches must come from one other pile. For example, if
a pile holds 6 matches, you may add 6 to it, no more or less.

You have three moves.

42. Tell "at a glance"

Here are two columns of numbers: 

	123456789        1
	12345678        21
	1234567        321
	123456 	      4321
	12345        54321
	1234        654321      
	123        7654321 
	12        87654321 
	1        987654321 

Look closely: the numbers on the right are the same as on the left, but
reversed and in reverse order. Which column has the larger total? (First
answer "at a glance"; then check by adding.) 

50. How Many Routes?

"In our Mathematics Circle we diagramed 16 blocks of our city. How many 
different routes can we draw from A to C moving only upward and to the right? 



Different routes may, of course, have portions that coincide (as in the
diagram).  

II. Difficult Problems

88. Cat and mice

A cat is taking a nap. He dreams he is encircled by 13 mice: 12 gray and 1
white. He hears his owner saying: "Cat: you are to eat each thirteenth
mouse, keeping the same direction. The last mouse you eat must be the white
one."

Which mouse should he start from? 

110. Knight's move

There are 16 pawns on a chessboard. 
Can a knight capture all 16 pawns in 16 moves? 

	. . . . . . . . 
	. . . . p p p . 
	. . . . p . p . 
	. . . . p p p . 
	. p p p . . . . 
	. p . p . . . . 
	. p p p . . . . 
	. . . . . . . .
	

147. Roses puzzle

(This version is a reconstruction of Kordemsky's problem 147, by
Will Shortz and Serhiy Grabarchuk]

Divide the square grid into four equal (and congruent) parts so that each
part contains exactly one each of the letters R, O, S, and E.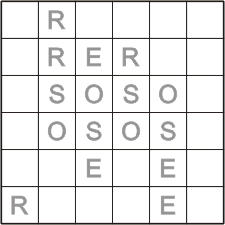

	    	

153. A Dissection Puzzle

Cut ABCDEF into 2 parts that can be fitted together as a square frame. The
opening in the frame should be a square congruent to each of the 3 squares
composing the original figure.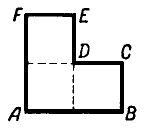

			

IX: Properties of Nine

A boy complained that he could not remember the multiplication table for
9. His father showed him how to help his memory with his fingers, like this:
Lay your hands palms down, extending your fingers. The fingers from left to
right are given numbers from 1 through 10, as shown. To find 9X7, lift the
number 7 finger. There are 6 fingers to its left and 3 to its right. Thus
9 X 7 = 63.



This works for multiplicands from 1 to 10, because these products of 9 have
digits that add up to nine (10 fingers, minus one not raised), and the
first digit is one less.

211. The Number 1,313

Ask a friend to write down this easily remembered number, subtract any number
from it, and make a five- to seven-digit number with the difference on the
left and 100 plus the number subtracted on the right. Now he crosses out any
nonzero digit and calls out the resulting number.

You promptly name the crossed-out digit.

What property of 1,313 simplifies your work?

332. Magic squares of order 4k

1. Number the cells consecutively:

		 1  2  3  4
		 5  6  7  8
		 9 10 11 12
	    	13 14 15 16

2. Divide the square with two vertical and two horizontal lines so that in
   each corner there is a square of order n/4 and in the center a square of
   order n/2.

3. Within these 5 squares, interchange all pairs of numbers symmetrically
   opposite the square's center. Outside the 5 squares, leave the numbers
   as they are.

		 16 2  3 13
		 5 11 10  8
		 9  7  6 12
	    	 4 14 15  1

Magic squares so formed are symmetric. 

In forming a magic square of order 4k, we reverse step 3. We leave the
numbers in the 5 squares as is. In the remaining four rectangles we
interchange all pairs of numbers symmetrically opposite the square's
center. Result: a magic square.

		 1 15  14 4
		12  6  7  9
		 8 10 11  5
	    	13  3  2 16
					p.155

Pandiagonal Magic Squares

5x5 pandiagonal (or diabolic) magic square:

	 1  8 15 17 24
	20 22  4  6 13
	 9 11 18 25  2
	23  5  7 14 16
	12 19  4  3 10

[follows a knights move + diagonal shift by 3 rule,
starting at corner]

All 8 diagonals also add up to 65. 

It has been proved that there are no diabolic squares of order (4k + 2), with
k an integer (for example, orders 6 and 10).

Diabolic squares exist for all other orders. 

					p.156

Contents

Introduction 						        vii
   I. Amusing Problems  				  	  1
  II. Difficult Problems 					 31
 III. Geometry with Matches 					 50
  IV. Measure Seven Times Before You Cut 			 59
   V. Skill Will Find Its Application Everywhere
  VI. Dominoes and Dice 					 82
 VII. Properties of Nine 					 91
VIII. With Algebra and without It 				 95
  IX. Mathematics with Almost No Calculations
   X. Mathematical Games and Tricks 				120
  XI. Divisibility 						135
 XII. Cross Sums and Magic Squares 				143
XIII. Numbers Curious and Serious 				157
 XIV. Numbers Ancient but Eternally Young 			173
 	Answers 						185
Index 303

Other reviews

physicsdatabase.com

to contribute some excerpts from your favourite book to book excerptise. send us a plain text file with page-numbered extracts from your favourite book. You can preface your extracts with a short review.
email to (bookexcerptise [at] gmail [dot] com).

We reply to all feedback!